2 The modeling language
The input to the ray tracer is a scene description (or
model) written in a functional modeling language called GML. The
language has a syntax and execution model that is similar to PostScript (and
Forth), but GML is lexically scoped and does not have side
effects.
2.1 Syntax
A GML program is written using a
subset of the printable ASCII character set (including space), plus tab, return,
linefeed and vertical tab characters. The space, tab, return, linefeed and
vertical tab characters are called whitespace.
The characters
%, [, ], {,
} are special characters.
Any occurrence of the
character ``%'' not inside a string literal (see below) starts a
comment, which runs to the end of the current line. Comments are treated as
whitespace when tokenizing the input file.
The syntax of GML is given in
Figure 1 (an
opt superscript means an optional item and a * superscript means a
sequence of zero or more items).
Figure 1: GML grammar
A GML program is a token list, which is a sequence
of zero or more token groups. A token group is either a single token, a
function (a token list enclosed in `{'
`}'), or an array (a token list enclosed in
`[' `]'). Tokens do not have to be separated by
white space when it is unambiguous. Whitespace is not allowed in numbers,
identifiers, or binders.
Identifiers must start with an letter and can
contain letters, digits, dashes (`-'), and underscores
(`_'). A subset of the identifiers are used as predefined
operators, which may not be rebound. A list of the operators can be
found in the appendix. A binder is an identifier prefixed with a
`/' character.
Booleans are either the literal
true or the literal false. Like operators,
true and false may not be
rebound.
Numbers are either integers or reals. The syntax of numbers is
given by the following grammar:
where a
DecimalNumber is a sequence of one or more decimal digits. Integers
should have at least 24-bits of precision and reals should be represented by
double-precision IEEE floating-point values.
Strings are written enclosed
in double quotes (`"') and may contain any printable character
other than the double quote (but including the space character). There are no
escape sequences.
2.2 Evaluation
We
define the evaluation semantics of a GML program using an abstract machine. The
state of the machine is a triple <ENV; a; c>, where ENV is an
environment mapping identifiers to values, a is a stack
of values, and c is a sequence of token groups. More formally, we
use the following semantic definitions:
|
| i |
in |
Int |
| i |
in |
BaseValue = Boolean È Int È
Real È String |
| v |
in |
Value = BaseValue È Closure È
Array È Point È Object È
Light |
| (ENV, c) |
in |
Closure = Env #
Code |
| a,[v1 ... vn] |
in |
Array = Value* |
| ENV |
in |
Env = Id -->
Value |
| a,b |
in |
Stack = Value* |
| c |
in |
Code = TokenList | |
Evaluation
from one state to another is written as <ENV; a; c> ==>
<ENV'; a'; c'> . We define ==>* to be the transitive closure of ==>. Figure 2 gives
the GML evaluation rules.
< ENV; a; i c> ==>
< ENV; a i; c>
(1) |
< ENV; a v; /x c>
==> < ENV±{ x :=
v}; a; c>
(2) |
< ENV; a; x c>
==> < ENV; a ENV( x); c>
(3) |
< ENV; a; {c'} c>
==> < ENV; a ( ENV,
c'); c>
(4) |
|
|
<ENV'; a; c'>
==>*
<ENV''; b; Ø> |
|
|
|
<ENV; a (ENV',
c'); apply c>
==> <ENV; b; c>
| |
(5) | |
|
|
<ENV; Ø; c'>
==>*
<ENV'; v1 ... vn; Ø> |
|
|
|
<ENV; a; [c'] c>
==> <ENV; a [v1 ... vn]; c>
| |
(6) | |
|
|
<ENV1; a; c1> ==>* <ENV''; b; Ø> |
|
|
| <ENV;
a true (ENV1, c1) (ENV2, c2);
if c> ==>
<ENV; b; c>
| |
(7) | |
|
|
<ENV2; a; c2> ==>* <ENV''; b; Ø> |
|
|
| <
ENV; a false (ENV1, c1) (ENV2, c2);
if c> ==>
<ENV; b; c>
| |
(8) | |
|
| a OPERATOR a' |
|
|
|
<ENV; b a; OPERATOR c>
==> <ENV; b a'; c>
| |
(9) | |
Figure 2: Evaluation rules for GML
In these rules, we write stacks with the top to the right
(e.g.; a x is a stack with
x as its top element) and token sequences are written with the first
token on the left. We use Ø to signify the empty stack and the empty code
sequence.
Rule 1
describes the evaluation of a literal token, which is pushed on the stack. The
next two rules describe the semantics of variable binding and reference.
Rules 4
and 5
describe function-closure creation and the apply operator. Rule 6
describes the evaluation of an array expression; note that body of the array
expression is evaluated on an initially empty stack. The semantics of the
if operator are given by Rules 7 and 8. The last
evaluation rule (Rule 9)
describes how an operator (other than one of the control operators) is
evaluated. We write
a OPERATOR a'
to mean that the operator OPERATOR
transforms the stack a to the stack a'. This notation is used below to specify the GML
operators.
We write Eval(c,
v1, ..., vn) = (v'1, ..., v'n) for when a program c yields
(v'1, ..., v'n) when applied to the values
v1, ..., vn; i.e., when
<{}; v1 ··· vn; c> ==>* <ENV; v'1 ···,v'n; Ø> .
There is no direct support for
recursion in GML, but one can program recursive functions by explicitly passing
the function as an extra argument to itself (see Section 2.7 for
an example).
2.3 Control operators
GML contains two control operators that can be
used to implement control structures. These operators are formally defined in Figure 2, but we
provide an informal description here.
The apply operator takes a
function closure, (ENV, c), off the stack and
evaluates c using the environment ENV and the
current stack. When evaluation of c is complete (i.e.,
there are no more instructions left), the previous environment is restored and
execution continues with the instruction after the apply. Argument and
result passing is done via the stack. For example: 1 { /x x x } apply addi
will evaluate to 2. Note that functions bind their variables according to
the environment where they are defined; not where they are applied. For example
the following code evaluates to 3: 1 /x % bind x to 1
{ x } /f % the function f pushes the value of x
2 /x % rebind x to 2
f apply x addi
The if operator takes two closures and a boolean off the stack
and evaluates the first closure if the boolean is true, and the second if
the boolean is false. For example, b { 1 } { 2 } if
will result in 1 on the top of the stack if b is true, and 2
if it is false
2.4 Numbers
GML
supports both integer and real numbers (which are represented by IEEE
double-precision floating-point numbers). Many of the numeric operators have
both integer and real versions, so we combine their descriptions in the
following:
- n1 n2 addi/addf n3
- computes the sum n3 of the numbers
n1 and n2.
- r1 acos r2
- computes the arc cosine r2 in
degrees of r1. The result is undefined
if r1 < -1 or 1 <
r1.
- r1 asin r2
- computes the arc sine r2 in degrees
of r1. The result is undefined if
r1 < -1 or 1 < r1.
- r1 clampf r2
- computes r2 = {
| 0.0 |
r1 <
0.0 |
| 1.0 |
r1 >
1.0 |
| r1 |
otherwise |
..
- r1 cos r2
- computes the cosine r2 of
r1 in degrees.
- n1 n2 divi/divf n3
- computes the quotient n3 of dividing
the number n1 by n2. The divi operator rounds its result towards 0.
For the divi operator, if n2 is
zero, then the program halts. For divf, the effect of division by
zero is undefined.
- n1 n2 eqi/eqf b
- compares the numbers n1 and
n2 and pushes true if
n1 is equal to n2; otherwise false is pushed.
- r floor i
- converts the real r to the greatest integer i that is less
than or equal to r.
- r1 frac r2
- computes the fractional part r2 of
the real number r1. The result
r2 will always have the same sign as the
argument r1.
- n1 n2 lessi/lessf b
- compares the numbers n1 and
n2 and pushes true if
n1 is less than n2; otherwise false is pushed.
- i1 i2 modi i3
- computes the remainder i3 of
dividing i1 by i2. The following relation holds between divi and
modi:
i2
(i1 divi i2) +
(i1 mod i2) = i1
- n1 n2 muli/mulf n3
- computes the product n3 of the
numbers n1 and n2.
- n1 negi/negf n2
- computes the negation n2 of the
number n1.
- i real r
- converts the integer i to its real representation r.
- r1 sin r2
- computes the sine r2 of
r1 in degrees.
- r1 sqrt r2
- computes the square root r2 of
r1. If r1 is negative, then the interpreter should halt.
- n1 n2 subi/subf n3
- computes the difference n3 of
subtracting the number n2 from
n1.
2.5 Points
A
point is comprised of three real numbers. Points are used to represent
positions, vectors, and colors (in the latter case, the range of the components
is restricted to [0.0, 1.0]). There are four operations on points:
- p getx x
- gets the first component x of the point p.
- p gety y
- gets the second component y of the point p.
- p getz z
- gets the third component z of the point p.
- x y z point p
- creates a point p from the reals x, y, and z.
2.6 Arrays
There are
two operations on arrays:
- arr i get vi
- gets the ith element of the array arr. Array indexing
is zero based in GML. If i is out of bounds, the GML interpreter should
terminate.
- arr length n
- gets the number of elements in the array arr.
The
elements of an array do not have to have the same type and arrays can be used to
construct data structures. For example, we can implement lists using two-element
arrays for cons cells and the zero-length array for nil. [] /nil
{ /cdr /car [ car cdr ] } /cons
We can also write a function that ``pattern matches'' on the head
of a list. { /if-cons /if-nil /lst
lst length 0 eqi
if-nil
{ lst 0 get lst 1 get if-cons apply }
if
}
2.7 Examples
Some simple function definitions written in GML: { } /id % the identity function
{ 1 addi } /inc % the increment function
{ /x /y x y } /swap % swap the top two stack locations
{ /x x x } /dup % duplicate the top of the stack
{ dup apply muli } /sq % the squaring function
{ /a /b a { true } { b } if } /or % logical-or function
{ /p % negate a point value
p getx negf
p gety negf
p getz negf point
} /negp
A more substantial example is the GML version of the recursive factorial
function: { /self /n
n 2 lessi
{ 1 }
{ n 1 subi self self apply n muli }
if
} /fact
Notice that this function follows the convention of passing itself as the
top-most argument on the stack. We can compute the factorial of 12 with
the expression 12 fact fact apply
3 Ray tracing
In this
section, we describe how the GML interpreter supports ray tracing.
3.1 Coordinate systems
GML models are defined
in terms of two coordinate systems: world coordinates and object
coordinates. World coordinates are used to specify the position of lights
while object coordinates are used to specify primitive objects. There are six
transformation operators (described in Section 3.3)
that are used to map object space to world space.
The world-coordinate
system is left-handed. The X-axis goes to the right, the
Y-axis goes up, and the Z-axis goes away from the viewer.
3.2 Geometric primitives
There are five operations in GML for constructing
primitive solids: sphere, cube, cylinder,
cone, and plane. Each of these operations takes a single
function as an argument, which defines the primitive's surface properties (see
Section 3.6).
- surface sphere obj
- creates a sphere of radius 1 centered at the origin with surface
properties specified by the function surface. Formally, the
sphere is defined by x2 +
y2 + z2 £ 1.
- surface cube obj
- creates a unit cube with opposite corners (0,0,0) and (1,1,1). The
function surface specifies the cube's surface properties.
Formally, the cube is defined by 0 £ x £ 1, 0 £ y £ 1, and 0 £ z £ 1. Cubes are a Tier-2 feature.
- surface cylinder obj
- creates a cylinder of radius 1 and height 1 with surface properties
specified by the function surface. The base of the cylinder is
centered at (0, 0, 0) and the top is centered at (0, 1, 0) (i.e., the
axis of the cylinder is the Y-axis). Formally, the cylinder is defined
by x2 + z2 £ 1 and 0 £ y £ 1. Cylinders are a Tier-2 feature.
- surface cone obj
- creates a cone with base radius 1 and height 1 with surface properties
specified by the function surface. The apex of the cone is at
(0, 0, 0) and the base of the cone is centered at (0, 1, 0). Formally, the
cone is defined by x2 +
z2 - y2 £ 0 and 0 £ y £ 1. Cones are a Tier-2 feature.
- surface plane obj
- creates a plane object with the equation y = 0 with surface
properties specified by the function surface. Formally, the
plane is the half-space y £ 0.
3.3 Transformations
Fixed size objects at the origin are not very
interesting, so GML provides transformation operations to place objects
in world space. Each transformation operator takes an object and one or more
reals as arguments and returns the transformed object. The operations are:
- obj rtx rty rtz translate obj'
- translates obj by the vector (rtx, rty, rtz). I.e., if obj is at
position (px, py, pz), then obj' is at position
(px+rtx, py+rty, pz+rtz).
- obj rsx rsy rsz scale obj'
- scales obj by rsx in the X-dimension,
rsy in the
Y-dimension, and rsz in the Z dimension.
- obj rs uscale obj'
- uniformly scales obj by rs in each dimension. This operation is called
Isotropic scaling.
- obj q rotatex obj'
- rotates obj around the X-axis by q degrees. Rotation is measured counterclockwise when
looking along the X-axis from the origin towards +¥.
- obj q rotatey obj'
- rotates obj around the Y-axis by q degrees. Rotation is measured counterclockwise when
looking along the Y-axis from the origin towards +¥.
- obj q rotatez obj'
- rotates obj around the Z-axis by q degrees. Rotation is measured counterclockwise when
looking along the Z-axis from the origin towards +¥.
For example, if we want to put a sphere of
radius 2.0 at (5.0, 5.0, 5.0), we can use the following GML code: { ... } sphere
2.0 uscale
5.0 5.0 5.0 translate
The first line creates the sphere (as described in Section 3.2, the
sphere operator takes a single function argument). The second line
uniformly scales the sphere by a factor of 2.0, and the third line translates
the sphere to (5.0, 5.0, 5.0).
These transformations are all
affine transformations and they have the property of preserving the
straightness of lines and parallelism between lines, but they can alter the
distance between points and the angle between lines. Using homogeneous
coordinates, these transformations can be expressed as multiplication by a
4#4 matrix. Figure 3
describes the matrices that correspond to each of the transformation operators.
[
| 1 |
0 |
0 |
|
| 0 |
1 |
0 |
|
| 0 |
0 |
1 |
|
| 0 |
0 |
0 |
1 | ] |
[
|
|
0 |
0 |
0 |
| 0 |
|
0 |
0 |
| 0 |
0 |
|
0 |
| 0 |
0 |
0 |
1 | ] |
[
| rs |
0 |
0 |
0 |
| 0 |
rs |
0 |
0 |
| 0 |
0 |
rs |
0 |
| 0 |
0 |
0 |
1 | ] |
| Translation |
Scale matrix |
Isotropic scale matrix |
| |
[
| 1 |
0 |
0 |
0 |
| 0 |
cos(q) |
-sin(q) |
0 |
| 0 |
sin(q) |
cos(q) |
0 |
| 0 |
0 |
0 |
1 | ] |
[
| cos(q) |
0 |
sin(q) |
0 |
| 0 |
1 |
0 |
0 |
| -sin(q) |
0 |
cos(q) |
0 |
| 0 |
0 |
0 |
1 | ] |
[
| cos(q) |
-sin(q) |
0 |
0 |
| sin(q) |
cos(q) |
0 |
0 |
| 0 |
0 |
1 |
0 |
| 0 |
0 |
0 |
1 | ] |
| Rotation (X-axis) |
Rotation (Y-axis) |
Rotation
(Z-axis) |
Figure 3: Transformation matrices
For example, translating the point (2.6, 3.0, -5.0) by (-1.6,
-2.0, 6.0) is expressed as the following multiplication:
|
é
ê
ê
ê
ë |
| 1.0 |
0.0 |
0.0 |
-1.6 |
| 0.0 |
1.0 |
0.0 |
-2.0 |
| 0.0 |
0.0 |
1.0 |
6.0 |
| 0.0 |
0.0 |
0.0 |
1.0 | |
ù
ú
ú
ú
û | |
|
é
ê
ê
ê
ë |
|
ù
ú
ú
ú
û |
= |
é
ê
ê
ê
ë |
|
ù
ú
ú
ú
û |
Observe
that points have a fourth coordinate of 1, whereas vectors have a fourth
coordinate of 0. Thus, translation has no effect on vectors.
3.4 Illumination model
When the ray that shoots from the eye position through
a pixel hits a surface, we need to apply the illumination equation to determine
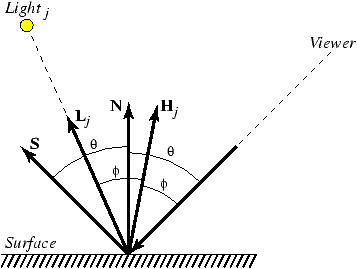
what color the pixel should have. Figure 4 shows
a situation where a ray from the viewer has hit a surface.
Figure 4: A ray intersecting a surface
The illumination at this point is given by the following
equation:
|
I = kd
Ia C +
kd |
|
(N·L |
j) Ij C + ks |
|
(N·Hj)n
Ij C +
ks Is C
(10) |
where
|
| C |
= |
surface color |
| Ia |
= |
intensity of ambient lighting |
| kd |
= |
diffuse reflection coefficient |
| N |
= |
unit surface normal |
| Lj |
= |
unit vector in direction of jth light
source |
| Ij |
= |
intensity of jth light source |
| ks |
= |
specular reflection coefficient |
| Hj |
= |
unit vector in the direction halfway between
the viewer and Lj |
| n |
= |
Phong exponent |
| Is |
= |
intensity of light from direction
S | |
The
view vector, N, and S all lie in the same plane. The
vector S is called the reflection vector and forms same
angle with N as the vector to the viewer does (this angle is
labeled q in Figure 4).
Light intensity is represented as point in GML and multiplication of points is
component wise. The values of C, kd, ks,
and n are the surface properties of the object at the point of
reflection. Section 3.6
describes the mechanism for specifying these values for an
object.
Computing the contribution of lights (the Ij part of the above equation) requires casting a shadow ray from the intersection point to the
light's position. If the ray hits an object that is closer than the light, then
the light does not contribute to the illumination of the intersection
point.
Ray tracing is a recursive process. Computing the value of
Is requires shooting a ray in the
direction of S and seeing what object (if any) it intersects. To avoid
infinite recursion, we limit the tracing to some depth. The depth limit
is given as an argument to the render operator (see Section 3.8).
3.5 Lights
GML
supports three types of light sources: directional lights, point
lights and spotlights. Directional lights are assumed to be
infinitely far away and have only a direction. Point lights have a position and
an intensity (specified as a color triple), and they emit light uniformly in all
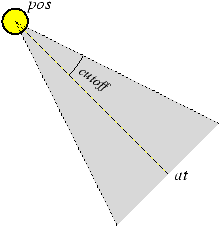
directions. Spotlights emit a cone of light in a given direction. The light cone
is specified by three parameters: the light's direction, the light's cutoff
angle, and an attenuation exponent (see Figure 5).
Figure 5: Spotlight
Unlike geometric objects, lights are defined in terms of
world coordinates.
- dir color light l
- creates a directional light source at infinity with direction
dir and intensity color. Both dir
and color are specified as point values.
- pos color pointlight l
- creates a point-light source at the world coordinate position
pos with intensity color. Both pos
and color are specified as point values. Pointlights are a Tier-2 feature.
- pos at color cutoff exp spotlight l
- creates a spotlight source at the world coordinate position
pos pointing towards the position at. The light's
color is given by color. The spotlight's cutoff angle is given
in degrees by cutoff and the attenuation exponent is given by
exp (these are real numbers). The intensity of the light from a
spotlight at a point Q is determined by the angle between the light's
direction vector (i.e., the vector from pos to
at) and the vector from pos to Q. If the
angle is greater than the cutoff angle, then intensity is zero; otherwise the
intensity is given by the equation
| I = |
æ
ç
ç
è |
|
|
· |
|
|
ö
÷
÷
ø |
|
color
(11) |
Spotlights are a
Tier-3
feature.
The light from point lights and spotlights is attenuated by
the distance from the light to the surface. The attenuation equation is:
where
d is the distance from the light to the surface and I is the
intensity of the light. Thus at a distance of 5 units the strength of the light
will be about 85% and at 10 units it will be about 50%. Note that the light
reflected from surfaces (the ks
Is C term in
Equation 3.4) is
not attenuated; nor is the light from directional sources.
3.6 Surface functions
GML uses procedural texturing to describe the
surface properties of objects. The basic idea is that the model provides a
function for each object, which maps positions on the object to the surface
properties that determine how the object is illuminated (see Section 3.4).
A
surface function takes three arguments: an integer specifying an object's face
and two texture coordinates. For all objects, except planes, the texture
coordinates are restricted to the range 0 £
u,v £ 1. The Table 1
specifies how these coordinates map to points in object-space for the various
builtin graphical objects.
Table 1: Texture coordinates for primitives
|
|
| SPHERE |
|
|
| (0, u, v) |
(sqrt(1 - y2)sin(360 u), y, sqrt(1 -
y2)cos(360 u)), |
where y = 2 v - 1 |
|
|
| CUBE |
|
|
| (0, u, v) |
(u, v, 0) |
front |
| (1, u, v) |
(u, v, 1) |
back |
| (2, u, v) |
(0, v, u) |
left |
| (3, u, v) |
(1, v, u) |
right |
| (4, u, v) |
(u, 1, v) |
top |
| (5, u, v) |
(u, 0, v) |
bottom |
|
|
| CYLINDER |
|
|
| (0, u, v) |
(sin(360 u), v, cos(360
u)) |
side |
| (1, u, v) |
(2 u - 1, 1, 2 v - 1) |
top |
| (2, u, v) |
(2 u - 1, 0, 2 v - 1) |
bottom |
|
|
| CONE |
|
|
| (0, u, v) |
(v sin(360 u), v, v
cos(360 u)) |
side |
| (1, u, v) |
(2 u - 1, 1, 2 v - 1) |
base |
|
|
| PLANE |
|
|
| (0, u, v) |
(u, 0, v) |
|
|
Note that (as always in GML), the arguments to the sin and
cos functions are in degrees. The GML implementation is responsible for the
inverse mapping; i.e., given a point on a solid, compute the texture
coordinates.
A surface function returns a point representing the surface
color (C), and three real numbers: the diffuse reflection coefficient
(kd), the specular reflection
coefficient (ks), and the Phong
exponent (n). For example, the code in Figure 6
defines a cube with a matte 3#3 black and white checked pattern on each face.
0.0 0.0 0.0 point /black
1.0 1.0 1.0 point /white
[ % 3x3 pattern
[ black white black ]
[ white black white ]
[ black white black ]
] /texture
{ /v /u /face % bind parameters
{ % toIntCoord : float -> int
3.0 mulf floor /i % i = floor(3.0*r)
i 3 eqi { 2 } { i } if % make sure i is not 3
} /toIntCoord
texture u toIntCoord apply get % color = texture[u][v]
v toIntCoord apply get
1.0 % kd = 1.0
0.0 % ks = 0.0
1.0 % n = 1.0
} cube
Figure 6: A checked pattern on a cube
3.7 Constructive solid geometry
Solid objects may be combined using boolean set operations to
form more complex solids. There are three composition operations:
- obj1 obj2 union obj3
- forms the union obj3
of the two solids obj1 and
obj2.
- obj1 obj2 intersect obj3
- forms the intersection obj3 of the two solids obj1 and obj2.
The intersect operator is a Tier-3 feature.
- obj1 obj2 difference obj3
- forms the solid obj3 that is
the solid obj1 minus the solid
obj2. The difference
operator is a Tier-3 feature.
We can determine the intersection of a ray and a compound solid by
recursively computing the intersections of the ray and the solid's pieces (both
entries and exits) and then merging the information according to the boolean
composition operator. Figure 7 illustrates
this process for two objects (this picture is called a Roth diagram).
Figure 7: Tracing a ray through a compound solid
When rendering a composite object, the surface properties are
determined by the primitive that defines the surface. If the surfaces of two
primitives coincide, then which primitive defines the surface properties is
unspecified.
3.8 Rendering
The
render operator causes the scene to be rendered to a file.
- amb lights obj depth fov
wid ht file
render ---
The render operator renders a scene to a file. It takes eight
arguments:
- amb
- the intensity of ambient light (a point).
- lights
- is an array of lights used to illuminate the scene.
- obj
- is the scene to render.
- depth
- is an integer limit on the recursive depth of the ray tracing owing to
specular reflection. I.e., when depth = 0, we do not recursively
compute the contribution from the direction of reflection (S in
Figure 4).
- fov
- is the horizontal field of view in degrees (a real number).
- wid
- is the width of the rendered image in pixels (an integer).
- ht
- is the height of the rendered image in pixels (an integer).
- file
- is a string specifying output file for the rendered image.
The
render operator is the only GML operator with side effects
(i.e., it modifies the host file system). A GML program may contain
multiple render operators (for animation effects), but the order in
which the output files are generated is implementation dependent. The results of
evaluating the render operator during the evaluation of a surface
function are undefined (i.e., your program may choose to exit with an
error, or execute the operation, or do something else).
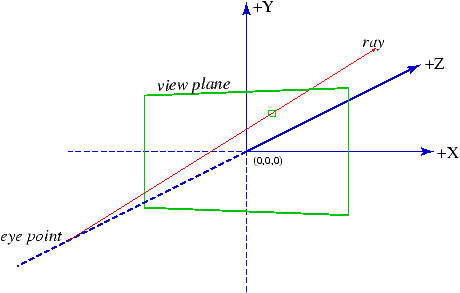
When rendering a
scene, the eye position is fixed at (0, 0, -1) looking down the Z-axis
and the image plane is the XY-plane (see Figure 8). The
horizontal field of view (fov) determines the width of the image
in world space (i.e., it is 2 tan(0.5 fov)), and the
height is determined from the aspect ratio. If the upper-left corner of the
image is at (x, y, 0) and the width of a pixel is D, then the ray through the jth pixel in the
ith row has a direction of (x + (j+0.5)D, y - (i+0.5)D, 1).
Figure 8: View coordinate system
When the render operation detects that a ray has intersected
the surface of an object, it must compute the texture coordinates at the point
of intersection and apply the surface function to them. Let (face,
u, v) be the texture coordinates and surf be the
surface function at the point of intersection, and let
Eval(surf apply,
face, u, v) = (C, kd, ks,
n)
Then the surface properties for the illumination equation (see
Section 3.4) are
C, kd, ks, and n.
3.9 The output format
The output format is the Portable Pixmap (PPM)
file format.1 The format consists of a ASCII
header followed by the pixel data in binary form. The format of the header is
- The magic number, which are the two characters ``P6.''
- A width, formatted as ASCII characters in decimal.
- A height, again in ASCII decimal.
- The ASCII text ``255,'' which is the maximum color-component
value.
These items are separated by whitespace (blanks, TABs, CRs, and
LFs). After the maximum color value, there is a single whitespace character
(usually a newline), which is followed by the pixel data. The pixel data is a
sequence of three-byte pixel values (red, green, blue) in row-major order. Light
intensity values (represented as GML points) are converted to RGB format by
clamping the range and scaling.
In the header, characters from a
``#'' to the next end-of-line are ignored (comments). This comment
mechanism should be used to include the group's name immediately following the
line with the magic number. For example, the sample implementation produces the
following header: P6
# GML Sample Implementation
256 256
255
5 Hints
5.1 Basic facts
The dot product of two
vectors v1 = (x1, y1,
z1) and v2 = (x2,
y2, z2) is v1·v2 = (x1 x2 +
y1 y2 + z1
z2). When v1 and v2 are
unit vectors, then v1·v2 is the cosine of the
angle formed by the two vectors. More generally, v1·v2 = |v1|
|v2| cos(q),
where q is the angle between the vectors.
5.2 Intersection testing
A plane P can
be defined by its unit normal Pn and the distance d from the plane to the
origin. The half-space that P = (Pn, d) defines are those points Q such
that Q·Pn + d £ 0. Given this
definition, the intersection of a ray R(t) =
(Ro + t
Rd) and a plane
(Pn, d) is given by
the equation
If
Pn·Rd = 0, then
the ray is parallel to the plane (it might lie in the plane, but we can ignore
that case for our purposes). If tintersection < 0, then the line defined by
the ray intersects the plane behind the ray's origin; otherwise the point of
intersection is R(tintersection). We can tell which side of the
plane Ro lies by examining
the sign of Pn·Rd; if it is
positive, then Ro is in the
half-space defined by P.
Computing the intersection of a ray
R(t) = (Ro + t Rd) and a sphere S centered at
Sc with radius r is
more complicated. Let loc be
the length of the vector from the ray's origin to the center of the sphere; then
if loc < r, the
ray originates inside the sphere. We can compute the distance along the ray from
the ray's origin to the closest approach to the sphere's center by the equation
tca =
(Sc -
Ro)·Rd (see Figure 9).
If tca < 0, then the ray
is pointing away from the sphere's center, which means that if the ray's origin
is outside the sphere then there is no intersection. Once we have computed
tca, we can compute the
square of the distance from the ray to the center at the point of closest
approach by the d2 = loc2 -
tca2. From this, we can compute the square of the half chord
distance thc2 = r2 -
d2 = r2 - loc2 +
tca2. As can be seen in Figure 9,
if thc<0, then the ray
does not intersect the sphere, otherwise the points of intersection are given by
R(tca±thc) (assuming the ray originates outside the
sphere).
Figure 9: Ray/sphere intersection
The intersection of a ray and a cube can be determined by
using the technique given for planes (test against the planes containing the
faces of the cube). Intersections for cones and cylinders can be determined by
plugging the ray equation (R(t) = Ro + t Rd) into the equations for the surface. In both cases
(as for spheres) the solution requires pluggin values into the quadratic
formula.
One approach to ray tracing with a modeling language that
supports affine transformations (such as GML) is to transform the rays into
object space and do the intersection tests there. This approach allows the
intersection tests to be specialized to the standard objects, which can greatly
simplify the tests. Remember, however, that affine transformations do not
preserve lengths --- applying an affine transformation to a unit vector will not
yield a unit vector in general.
5.3 Surface acne
One
problem that you are likely to encounter is called surface acne and
results from precision errors. The problem arises from when the origin of a shadow ray is
on the wrong side of its originating surface, and thus intersets the surface.
The visual result is usually a black dot at that pixel. The sample images
include an example that illustrates this problem. One solution is to offset the
shadow ray's origin by a small amount in the ray's direction. Another solution
is not to test intersection's against the originating surface.
5.4 Optimizations
There are opportunities for
performance improvements both in the the implementation of the GML interpreter
and in the ray tracing engine.
While the time spent to compute the
objects in a scene is typically small compared to the rendering time, the GML
functions that define the surface properties get evaluated for every ray
intersection. You may find it useful to analyse surface functions for the common
case where they are constant.
The resources listed below include
information on techniques for improving the efficiency of ray tracing. Most of
these techniques focus on reducing the cost or number of ray/solid intersection
tests. For example, if you precompute a bounding volume for a complex object,
then a quick test against the bounding volume may allow you to avoid a more
expensive test against the object. If your implementation supports the Tier-3
CSG operators, then you probably want to have a version of your intersection
testing code that is specialized for shadow
rays.
5.5 Resources
Here are a few pointers to
on-line sources of information about graphical algorithms and ray
tracing.
- http://www.cs.bell-labs.com/~jhr/icfp/examples.html
is a page of example GML specifications with the expected images.
- http://www.cs.bell-labs.com/~jhr/icfp/operators.txt
is a text file that lists all of the GML operators.
- http://www.realtimerendering.com/int/
is the 3D Object Intersection page with pointers to papers and code
describing various intersection algorithms.
- http://www.acm.org/tog/resources/RTNews/html/
is the home page of the Ray Tracing News, which is an online journal
about ray tracing techniques.
- http://www.cs.utah.edu/~bes/papers/fastRT/
is a paper by Brian Smits on efficiency issues in implementing ray tracers.
- http://www.acm.org/pubs/tog/GraphicsGems/
is the source-code repository for the Graphics Gems series.
- http://www.exaflop.org/docs/cgafaq/
is the FAQ for the comp.graphics.algorithms news group.
- http://www.magic-software.com
has source code for various graphical algorithms.
Operator summary
The following is an
alphabetical listing of the GML operators with brief descriptions. The third
column lists the section where the operator is defined and the fourth column
specifies which implementation tier the operator belongs to.